The continuous wavelet transfrom of a (possibly complex) signal 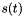$s(t)$ , given a mother wavelet 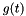$g(t)$ , at time 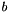$b$ and scale 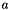$a$ is given by

$m(b,a) = \int_{-\infty}^{\infty}\bar{s}(t)\,\frac{1}{a}g\left(\frac{t-b}{a}\right)\,dt\,,$

see Wavelets for a list of all implemented wavelets. For each proper (analysis) wavelet[2] 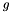$g$ , there exists a second (synthesis) wavelet 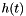$h(t)$ that reconstructs the signal as

$s(t) = \frac{1}{c_{g,h}}\,\int_{0}^{\infty}\,\frac{da}{a}\,\int_{-\infty}^{\infty}\,dt\, \bar{m}(b,a)\,\frac{1}{a}h\left(\frac{b-t}{a}\right)\,,$

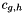where $c_{g,h}$ is a normalization constant depending on the chosen wavelet pair $g,h$ .

Efficient implementation of the continious wavelet transform.

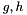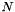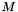In general, using the FFT convolution algorihtm to perform a wavelet transform of a signal of length $N$ at $M$ scales, the computational costs (time) are generally 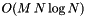$O(M\,N\log N)$ . Hence the tranform can get pretty slow for long signals. Exploiting, that wavelets are usually well localized in the time and frequency domain, allows for a significant reduction of the computational costs of the transform. 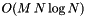This gain, however, is a constant factor which means, that the general dependency of the costs on the signal length and number of scales remains in the order of $O(M\,N\log N)$ .

The Morlet wavelet at different scales in time and frequency.

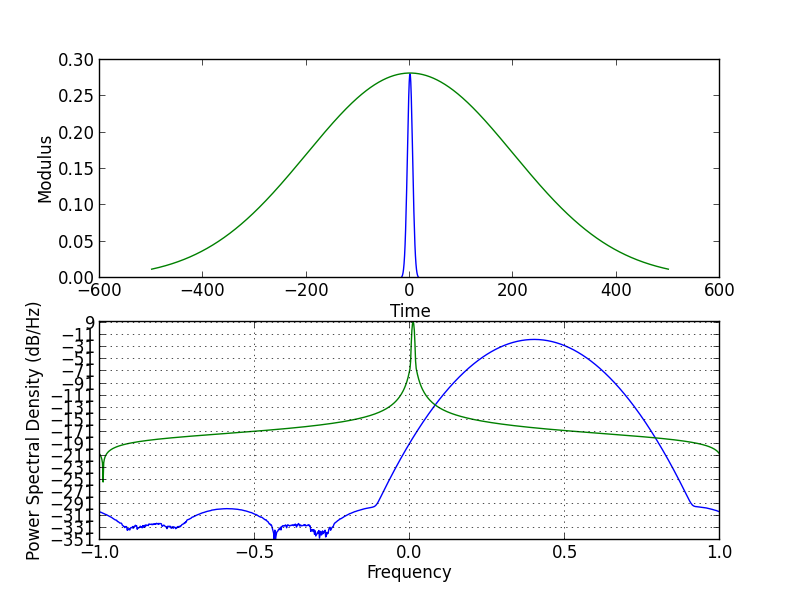
At small scales, the time localization of the wavelet can be exploited (see figure above, upper panel). There the scaled wavelet can be approximated well by a filter kernel beeing much shorter than the time series. The convolution of the (short) scaled wavelet with the (long) time series can then be performed efficiently by using the well known "overlap-add" method[3].

At large scales (figure above, lower panel), the frequency localization of the wavelet can be exploited. There the high-frequency components of the wavelet are basically zero and the convolution of these long but low-frequency wavelets can be performed in an interleaved manner on sub-samples of the signal. This approach is related to the "algorithm a trois"[1] for the wavelet transform on dyadic grids.

In both cases, a time series of length 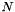$N$ will be processed in terms of 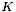$K$ signals of length 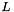$L$ , such that 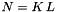$N = K\,L$ (assuming the signal length can be factored that way, if not the signal will be zero-padded). Hence the computational costs of the FFT convolutions to obtain a single "voice" (wavelet trasform at a specific frequency/scale) are 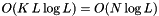$O(K\,L\log L)=O(N\log L)$ instead of 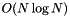$O(N\log N)$ . 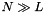If $N\gg L$ the costs of the wavelet transform can be reduced significantly.